本文共 5514 字,大约阅读时间需要 18 分钟。
1.背景
在了解这两种转换方法时,我们有必要先了解一些与此相关的基本知识。我们有三种常用的方式来表示空间坐标,分别是:经纬度和高层、平面坐标和高层以及空间直角坐标。
2.经纬度坐标系(大地坐标系)
这里我首先要强调:天文坐标表示的经纬度和大地坐标系表示的经纬度是不同的。所以,同一个经纬度数值,在BJ54和WGS84下表示的是不同的位置,而以下我说的经纬度均指大地坐标系下的经纬度。大地坐标系是大地测量中以参考椭球面为基准面建立起来的坐标系。下面我跟大家大致谈谈其中涉及到的两个重要概念。
2.1大地水准面和大地球体
地球表面本身是一个起伏不平、十分不规则的表面,这些高低不平的表面无法用数学公式表达,也无法进行运算,所以在量测和制图时,我们必须找一个规则的曲面来代替地球的自然表面。
当海洋静止时,它的自由水面必定与该面上各点的重力方向(铅垂直方向)成正交,我们把这个面叫做水准面。但是,地球上的水准面有无数个,我们把其中与静止的平均海水面相重合的水准面设想成一个可以将地球进行包裹的闭合曲面,这个水准面就是大地水准面。
而被大地水准面包裹所形成的球体即为大地球体。
2.2地球椭球体
由于地球体内部质量分布的不均匀,引起重力方向的变化,这个处处与重力方向成正交的大地水准面边成为了一个十分不规则的也不能用数学来表示的曲面。不过虽然大地水准面的形状十分的不规则,但它已经是一个很接近于绕自转轴(短轴)旋转的椭球体了。
所以在测量和制图中就用旋转椭球来代替大地球体,这个旋转球体通常称地球椭球体,简称椭球体。
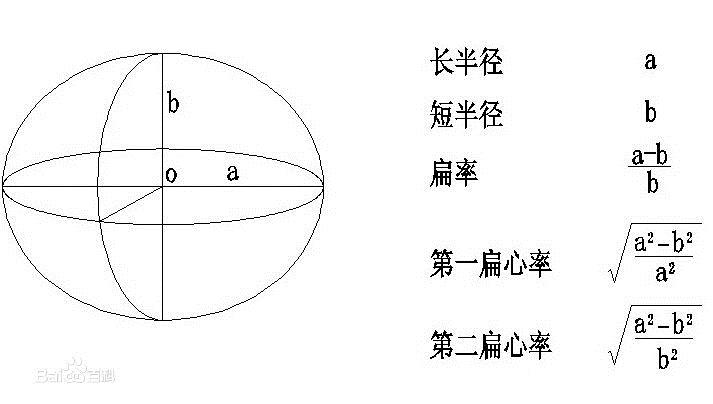
2.3常用大地坐标系
不同坐标系,其椭球体的长半径,短半径和扁率是不同的。比如我们常用的四种坐标系所对应的椭球体,它们的椭球体参数就各不相同:
BJ54坐标系:属参心坐标系,长轴6378245m,短轴6356863,扁率1/298.3。
XIAN80坐标系:属参心坐标系,长轴6378140m,短轴6356755,扁率1/298.25722101。WGS84坐标系:属地心坐标系,长轴6378137.000m,短轴6356752.314,扁率1/298.257223563。CGCS2000坐标系:属地心坐标系,长轴6378137.000m,短轴6356752.31414 ,扁率f = 1/ 298.257222101。
由上面的参数我们可以看出,对于大地坐标系,我们还可以分为两种:参心坐标系和地心坐标系。
2.3.1参心坐标系
“参心”意指参考椭球的中心。在测量中,为了处理观测成果和传算地面控制网的坐标,通常须选取一参考椭球面作为基本参考面,选一参考点作为大地测量的起算点(大地原点),利用大地原点的天文观测量来确定参考椭球在地球内部的位置和方向。参心大地坐标的应用十分广泛,它是经典大地测量的一种通用坐标系。根据地图投影理论,参心大地坐标系可以通过高斯投影计算转化为平面直角坐标系,为地形测量和工程测量提供控制基础。
BJ54坐标系是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系。其大地原点在前苏联的普尔科沃,东经30°19′15”,北纬59°46′6”。
XIAN80坐标系是以1975年国际大地测量与地球物理联合会第十六届大会推荐的数据作为地球椭球体。其大地原点在我国中部的陕西省泾阳县永乐镇,东经108°55′25.00″,北纬34°32′27.00″。

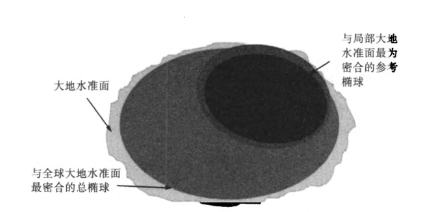
2.3.2地心坐标系
地心坐标系(geocentric coordinate system )以地球质心为原点建立的空间直角坐标系,或以球心与地球质心重合的地球椭球面为基准面所建立的大地坐标系。
其产生的原因是因为早起的参心坐标系虽然能很好的满足局部地区的测量需求,但是却无法满足全球定位的需求,原因是参心坐标系以跟局部大地水准面最吻合的椭球体作为参考椭球,而此参考椭球并不能符合全球定位的需求。所以在地心坐标系中,我们以与全球大地水准面最密合的椭球体作为参考椭球。
目前地心坐标系的测量主要是三种方式:重力测量法、卫星大地测量法以及局部坐标转换。我们所熟知的GPS定位和北斗定位均是卫星大地测量法。
2.3.3推论
a.地心坐标系更适合全球范围的测量。
b. WGS84下的坐标在CGCS2000坐标系下基本表示的是同一个坐标,精度差距是厘米级的。
c. 在同一个椭球里的转换都是严密的,而在不同的椭球之间的转换是不严密的。举个例子,在WGS-84坐标和北京54坐标之间是不存在一套转换参数可以全国通用的,在每个地方会不一样,因为它们是两个不同的椭球基准。
3.平面坐标系(投影坐标系)
首先我们必须明确,投影坐标系是建立在地理坐标系之上的。换句话说就是,必须先有地理坐标系下的坐标,才能对该坐标进行投影,从而得到投影坐标。
那么,为什么有地理坐标系和投影坐标系之分呢?
由于经纬度的度数不对应某一标准长度,因此无法精确测量距离或面积,也难以在平面地图或计算机屏幕上显示数据。在使用许多(不是全部)GIS 分析和制图应用程序时,经常需要由投影坐标系提供的更稳定的平面坐标框架。与地理坐标系不同,在二维空间范围内,投影坐标系的长度、角度和面积恒定。投影坐标系始终基于地理坐标系,而后者则是基于球体或旋转椭球体的。在投影坐标系中,通过格网上的 x,y 坐标来标识位置,其原点位于格网中心。
按照投影构成的方法,我们将投影分为两类:几何投影和非几何投影。在我们国内,最常见的投影为高斯克吕格投影,基本中国分省(区)地图的投影和大比例尺地图的投影均选择为高斯克吕格投影。而且,各种大、中比例尺地形图采用了不同的高斯-克吕格投影带。其中大于1∶1万的地形图采用3°带;1∶2.5万至1∶50万的地形图采用6°带。
3.1高斯克吕格投影(Gauss_Kruger)
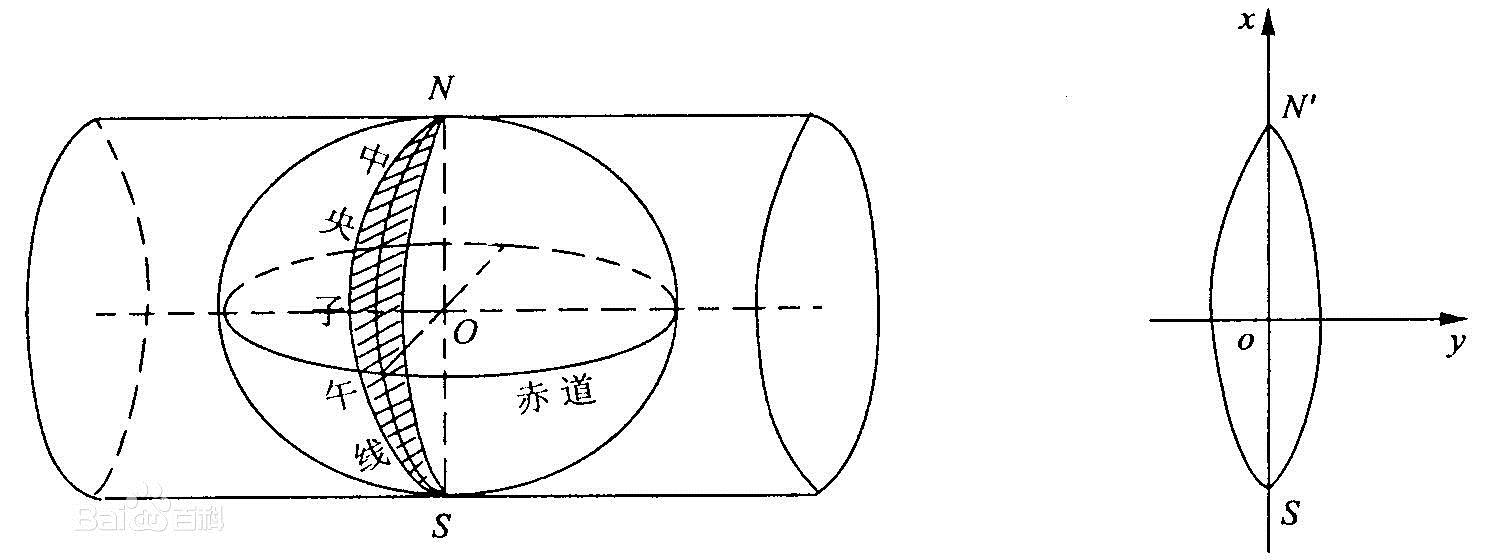
假想有一个椭圆柱面横套在地球椭球体外面,并与某一条子午线(此子午线称为中央子午线或轴子午线)相切,椭圆柱的中心轴通过椭球体中心,然后用一定投影方法,将中央子午线两侧各一定经差范围内的地区投影到椭圆柱面上,再将此柱面展开即成为投影面, 此投影为高斯投影。
高斯投影是正形投影的一种,隶属于几何投影。
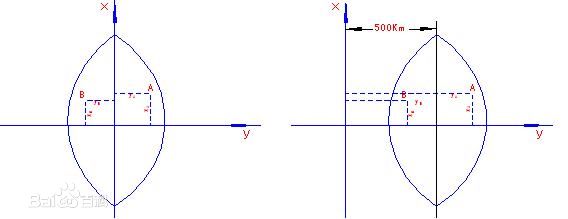
在投影面上,中央子午线和赤道的投影都是直线,并且以中央子午线和赤道
的交点0作为坐标原点,以中央子午线的投影为纵坐标x轴,以赤道的投影为横坐标y轴。在我国x坐标都是正的,y坐标的最大值(在赤道上6°带)约为330km。为了避免出现负的横坐标,可在横坐标上加上500 000m。此外还应在坐标前面再冠以带号。这种坐标称为国家统一坐标。 例如,有一点y=19 623 456.789m,该点位在19带内,位于中央子午线以东,其相对于中央子午线而言的横坐标则是:首先去掉带号,再减去500 000m,最后得=123 456.789m。
并且,由于采用了分带方法,各带的投影完全相同,某一坐标值(x,y),在某一投影中均有一个,在全球则有60个同样的坐标值,不能确切表示该点的位置。因此,在Y值前,需要冠以带号,这样的坐标称为通用坐标。
3.2高斯克吕格投影与UTM投影的对比
UTM投影全称为UNIVERSAL TRANSVERSE MERCATOL PROJECTION (通用横轴墨卡托投影),是一种“等角横轴割圆柱投影”,椭圆柱割地球于南纬80度、北纬84度两条等高圈,投影后两条相割的经线上没有变形,而中央经线上长度比0.9996。UTM投影是为了全球战争需要创建的,美国于1948年完成这种通用投影系统的计算。与高斯-克吕格投影相似,该投影角度没有变形,中央经线为直线,且为投影的对称轴,中央经线的比例因子取0.9996是为了保证离中央经线左右约330km处有两条不失真的标准经线。
UTM投影分带方法与高斯—克吕格投影相似,将北纬84度至南纬80度之间按经度分为60个带,每带6度.从西经180度起算,两条标准纬线距中央经线为180Km左右,中央经线比例系数为0.9996。我国的卫星影像资料常采用UTM投影。
从投影几何方式看,高斯-克吕格投影是“等角横切圆柱投影”( Transverse Tonformal Tylinder Projection),投影后中央经线保持长度不变,即比例系数为1;UTM投影是“等角横轴割圆柱投影”,圆柱割地球于南纬80度、北纬84度两条等高圈,投影后两条割线上没有变形,中央经线上长度比 0.9996。因此如果采用相同的椭球体,从计算结果看,两者主要差别在比例因子上,高斯-克吕格投影中央经线上的比例系数为1, UTM投影为0.9996,高斯-克吕格投影与UTM投影可近似采用 X[UTM]=0.9996 * X[高斯],Y[UTM]=0.9996 * Y[高斯],进行坐标转换(注意:如坐标纵轴西移了500000米,转换时必须将Y值减去500000乘上比例因子后再加500000)。从分带方式看,两者的分带起点不同,高斯-克吕格投影自0度子午线起每隔经差6度自西向东分带,第1带的中央经度为3°;UTM投影自西经180°起每隔经差6度自西向东分带,第1带的中央经度为-177°,因此高斯-克吕格投影的第1带是UTM的第31带。此外,两投影的东伪偏移都是500公里,高斯-克吕格投影北伪偏移为零,UTM北半球投影北伪偏移为零,南半球则为10000公里。
因此我们在进行测量、制图以及数据转换时,要注意二者的不同,避免产生误差,造成不必要的错误。
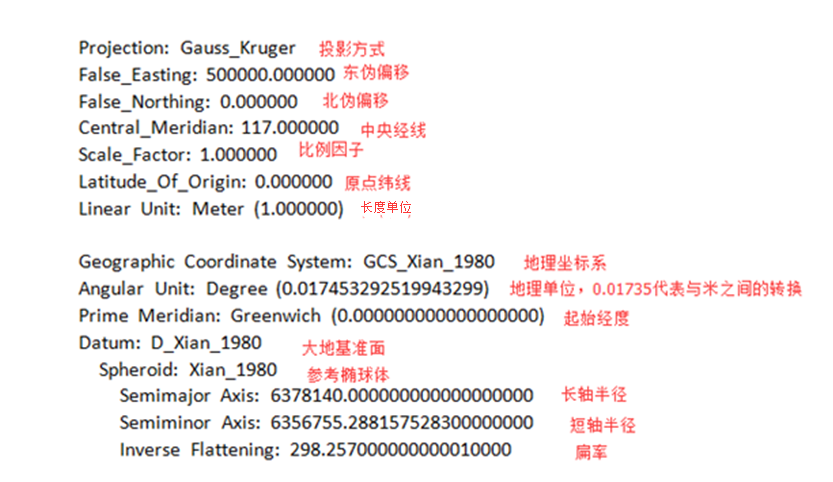
3.3 ArcGIS中坐标系的含义
ArcGIS中有地理坐标系(Geographic coordinate system)和投影坐标系(Projected coordinate system)两种。前者即是来定义使用何种地理坐标系的,而后者是同时定义地理坐标系和投影坐标系的。
如下为其中各个参数的含义:
4.七参数转换
在了解了上面三节所讲的内容后,我们来一起探讨项目中经常遇到的问题。首先的问题便是两个椭球体之间的转换,比如:WGS84的经纬度坐标转换到XIAN80的经纬度坐标。
4.1转换方法以及参数的获取
七参数法(包括布尔莎模型,一步法模型,海尔曼特等)是解决此问题的比较严密和通用的方法。其涉及到的七个参数为:X平移,Y平移,Z平移,X旋转,Y旋转,Z旋转,尺度变化K。此七个参数可以通过在需要转化的区域里选取3个以上的转换控制点对而获取。
如果区域范围不大,最远点间的距离不大于30Km(经验值),这可以用三参数(莫洛登斯基模型),即X平移,Y平移,Z平移,而此时将X旋转,Y旋转,Z旋转,尺度变化K视为0。所以三参数只是七参数的一种特例。三参数只需通过1个控制点对就能获取。
4.2详细解释各个参数的含义
a.三个坐标平移量(△X,△Y,△Z),即两个空间坐标系的坐标原点之间坐标差值;
b.三个坐标轴的旋转角度(△α,△β,△γ)),通过按顺序旋转三个坐标轴指定角度,可以使两个空间直角坐标系的XYZ轴重合在一起。c.尺度因子K,即两个空间坐标系内的同一段直线的长度比值,实现尺度的比例转换。通常K值几乎等于1。4.3注意
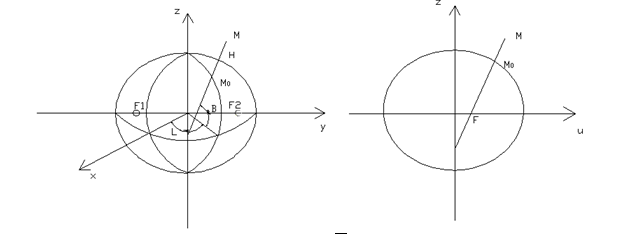
七参数转换是针对将地理坐标系所对应的空间直角坐标转换为另一坐标系的空间直接坐标。
空间直角坐标系的原点位于地球参考椭球的中心,Z轴与地球自转轴平行并指向参考椭球的北极,X轴指向参考椭球的本初子午线,Y轴与X轴和Z轴相互垂直最终构成一个右手系。大地坐标系是以大地基准为基础建立起来的,大地基准又以参考椭球为基础,由此大地坐标系又被称为椭球坐标系。
5.四参数转换
5.1转换方法及四参数的获取
在一个椭球的不同坐标系中的平面坐标之间转换转换则会用到平面转换。目前一般分为四参数和平面网格拟合两种方法,以四参数法在国内用的较多。
四参数的数学含义是:用含有四个参数的方程表示因变量(y)随自变量(x)变化的规律。
举个例子,在珠海既有北京54的平面坐标又有珠海的平面坐标,在这两种坐标之间转换就用到四参数。四参数的获取需要有两个控制点对。
当然,更精确的可以提供网格拟合数据,然后进行网格拟合。
5.2 四参数转换的数学意义
四参数模式为Y=(a-d)/[1+(x/c) ^b]+d
a:曲线上渐近线估值。
b:曲线的斜率。
c:最大结合一半时对应的剂量。
d:曲线下渐近线估值。
用迭代或逼近法解多元方程方程公式为:
Y=(A-D)/(1+(X/C)^B) + D
6.通过例子了解换算步骤
例子:在珠江一个测区,需要完成WGS-84坐标到珠江坐标系(54椭球)的坐标转换,其整个转换过程是:
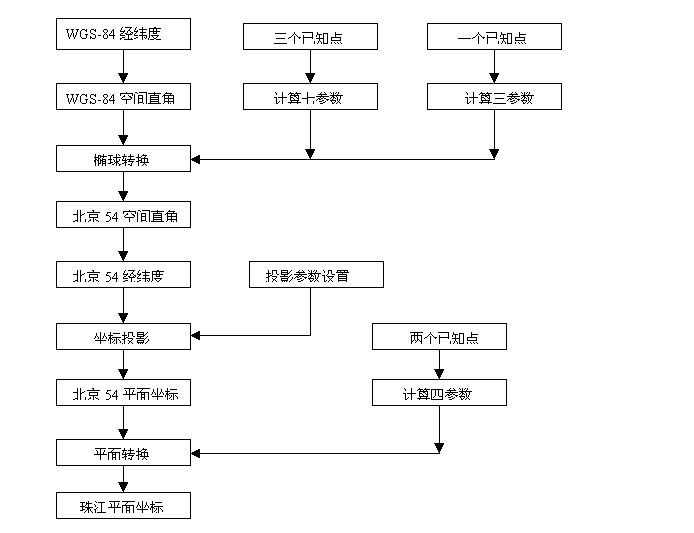
具体流程是:
a.将WGS84的经纬度转换为WGS84空间直角坐标系下的坐标。
b.用当地三个WGS84和当地坐标(椭球体为BJ54)之间的控制点对,获得七参数。
c.将WGS84的空间直角坐标利用七参数转换到BJ54坐标系下的空间直角坐标。
d.将BJ54的空间直角坐标转换为BJ54的经纬度坐标。
e.对此时BJ54的经纬度坐标进行高斯克吕格投影变为BJ54平面坐标。
f.用当地BJ54下的平面坐标和当地平面坐标之间的两个控制点对得出四参数。
g.将BJ54平面坐标利用四参数转换到当地平面坐标。
7.总结
写此篇文章查看了诸多资料。感谢Jack Deng的。感谢方庆林的,感谢博客园和知乎上的前辈。感谢乌伦老师的地理信息统原理一书。
此文中的高斯克吕格投影的正算和反算算法,以及七参数和四参数方法都能在网上找到,这里就不给大家一一贴出。
转载地址:http://bnnpo.baihongyu.com/